一个亟待解决的问题

对我来说，Kaspa 最有趣的地址之一是

 https://explorer.kastop.com/addresses/kaspa:qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqkx9awp4e 的所谓“销毁地址”。截至撰写本文时，包含大约 ~11M 的 KAS（价值 1.5M 美元）。它背后有一个非常有趣的故事，但我不会在本文中深入探讨。如果你对那个故事感兴趣，我建议你在 https://youtu.be/H-yiMbMV1ZI?t=225 观看 Kaspa Silver 的视频

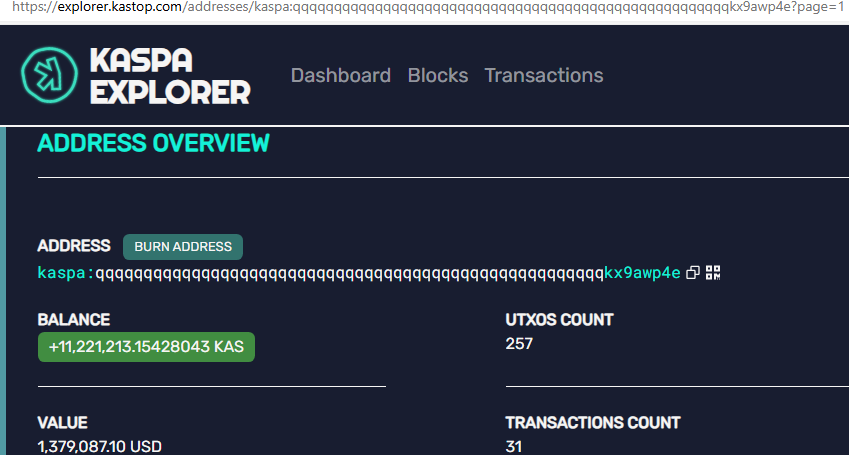
当我得知这个地址时，一个亟待解决的问题立刻进入了我的脑海：我们如何确定没有人秘密拥有这个地址的私钥，或者将来没有人会偶然发现它？

在本文中，我将介绍一些相关概念，并证明我是如何说服自己回答这个问题的。

无论如何，我们如何生成 Kaspa 地址？

Kaspa 使用 secp256k1 椭圆曲线生成地址。有一个生成器 （G） 点（众所周知的点，由标准预定义），您可以不断将其添加到自身中大量次，以到达曲线上的另一个点。您将到达的点代表您的公钥，您将 Generator 点添加到自身的次数就是您的私钥。然后以某种方式（使用 Bech32）对公钥进行编码，以生成您熟悉的地址格式 — 以 “kaspa：” 开头的地址。这个地址可以解码回公钥/点表示形式（这个解码过程实际上与验证数字签名有关）。我知道我在这里掩盖了很多实现细节，但重要的是：具有有效私钥的公钥必须是 secp256k1 椭圆曲线上的现有点。

Kaspa 有 3 种类型的地址：Schnorr P2PK 地址、ECDSA P2PK 地址和 P2SH 地址。这本身就是一个更广泛的话题，所以我只介绍相关部分。特别是销毁地址是 Schnorr P2PK 地址。对于 Schnorr P2PK 地址，我们只需要对曲线上公钥/点的 X 坐标部分进行编码即可。因此，如果你将销毁地址解码回它的公钥/点表示形式，你会发现销毁地址是某个 Y 的 （0， Y） 形式的点的编码。

关于 secp256k1 椭圆曲线的更多信息

此曲线的公式为：

Y² ≡ x³ + 7 （模 p）

其中 p = 2²⁵⁶ — 2³² — 977

这里的 p 是一些大的素数。该曲线在有限域 Zp 上定义，这意味着 X 和 Y 坐标是 256 位整数对大数 （p） 的模数。（来源： https://bitcoin.stackexchange.com/a/21911）.因此，对于此曲线中存在的点，X 和 Y 都必须是整数。

要了解有关此曲线的更多信息，请观看 Bitcoin Edge at https://www.youtube.com/watch?v=DcGm_4-ig1o 的精彩视频

我们知道这个地址是曲线中某个 Y 的 （0， Y） 形式的点的编码。假设曲线上有一个有效的点，我们必须能够找到一个满足上述方程的整数 Y，并确定它到底是什么点。

证据

由于我们知道销毁地址代表某个 Y 的点 （0， Y），因此我们可以尝试找到求解方程 y² ≡ x³ + 7 mod p 的 Y 值

代入 point 的值，我们得到：

y² ≡ 0³+ 7 （模 p）

或者简单地：

Y² ≡ 7 （Mod P）

事实证明，有一种简单的方法可以确定一个数字是否是素数的二次模余数：欧拉准则（来源：https：//en.wikipedia.org/wiki/Euler's_criterion）。

该标准说：

从本质上讲，假设存在 y² ≡ 7 （mod p） 的整数解，则以下必须为真：

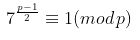
同样，p = 2²⁵⁶ — 2³² — 977 = 115792089237316195423570985008687907853269984665640564039457584007908834671663 — 确实是一个非常大的数字！

将这些值代入 Wolfram Alpha，我们得到：

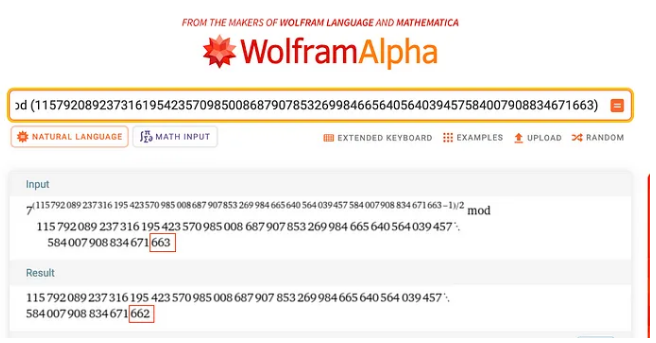
结果115792089237316195423570985008687907853269984665640564039457584007908834671662实际上等于 （p — 1），这意味着我们的欧拉准则方程实际上是：

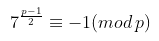
那么这意味着什么呢？根据欧拉准则，这意味着 y² ≡ 7 （mod p） 没有 y 的整数解。请记住，secp256k1 曲线仅针对 X 和 Y 都是整数的点 （X， Y） 定义。这意味着 （0， Y） 形式的点在任何 Y 的曲线上都不存在！私钥只能存在于曲线上的有效点，这意味着对于销毁地址 kaspa：qqqqqkx9awp4e 不能有任何与这个地址相关联的私钥——因为这个地址应该代表的点在 secp256k1 曲线上不存在！

令人满意的答案

回到我最初的问题“我们如何确定没有人秘密拥有这个地址的私钥，或者将来没有人可以偶然发现它？

答案是，在 secp256k1 曲线上，这个地址没有可能的私钥。不仅没有人知道私钥，而且没有人能知道它，因为它不存在。